
Данную методику решения судоку подготовила Nekonyash
Цель судоку – расставить все цифры так, чтобы в квадратах 3х3, строках и столбцах не было одинаковых цифр. Вот пример уже решенного судоку:
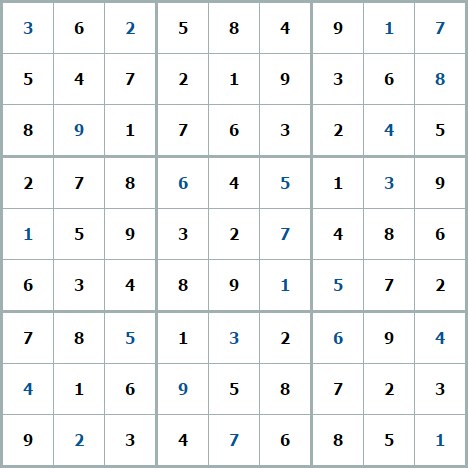
Можно проверить, что в каждом из девяти квадратов, а и так же во всех строках и столбцах нет повторяющихся чисел. Решая судоку нужно пользоваться этим правилом «уникальности» числа и, последовательно исключая кандидатов (маленькие числа в клетке обозначают какие числа, по мнению игрока, могут стоять в этой клетке), находить места, где может стоять только одно число.
Открыв судоку, мы видим, что в каждой клетке проставлены все маленькие серые числа. Можно сразу убрать отметки с уже выставленных чисел (отметки убираются щелчком правой мыши по маленькому числу):

Начну с числа, которое в данном кроссворде есть в одном экземпляре - 6, чтобы было удобнее показать исключение кандидатов.
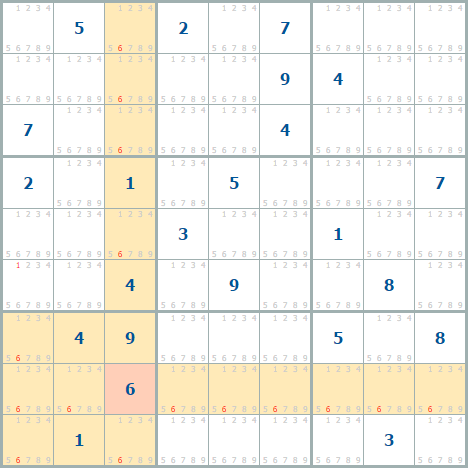
Числа исключаются в квадрате с числом, в строке и столбце, убираемые кандидаты отмечены красным – по ним мы и кликнем правой кнопкой мыши, отметив, что здесь шестерок в этих местах быть не может (иначе получится две шестерки в квадрате/столбце/строке, что противоречит правилам).
Теперь, если вернуться к единицам, то картина исключений будет следующей:
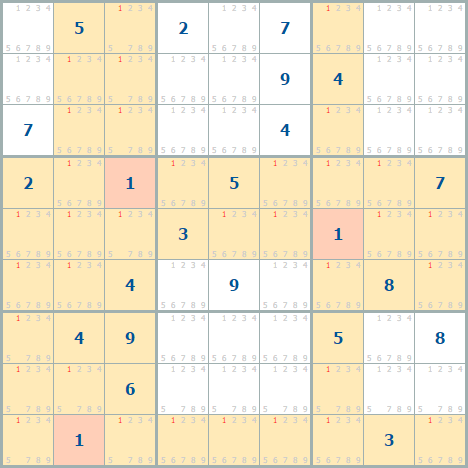
Мы убираем кандидаты 1 в каждой свободной клетке квадрата, где уже есть 1, в каждой строке, где есть 1 и в каждом столбце, где есть 1. Итого для трех единиц будет 3 квадрата, 3 столбца и 3 строки.
Далее перейдем сразу к 4, цифр больше, но принцип тот же. И если присмотреться, то видно, что в левом верхнем квадрате 3х3 остается всего одна свободная клетка (отмечена зеленым), где может стоять 4. Значит, ставим туда цифру 4 и стираем всех кандидатов (других чисел там стоять больше не может). В простых судоку таким образом можно заполнить довольно много полей.

После того, как выставлено новое число – можно перепроверить предыдущие, ведь добавление нового числа сужает круг поиска, например, в этом кроссворде благодаря выставленной четверке, под единицу в этом квадрате осталась всего одна клетка (зеленая):
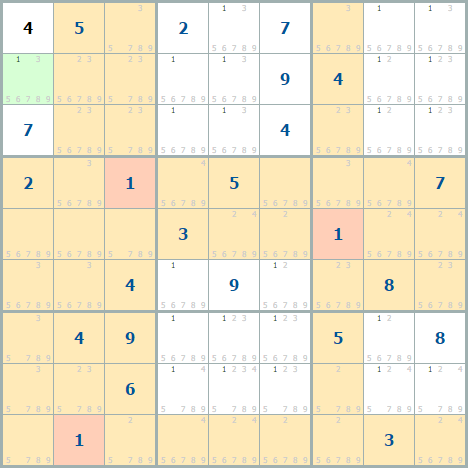
Из трех доступных клеток под единицу не занята всего одна, туда единицу и ставим.
Таким образом убираем всех очевидных кандидатов для всех чисел (от 1 до 9) и проставляем числа по возможности:
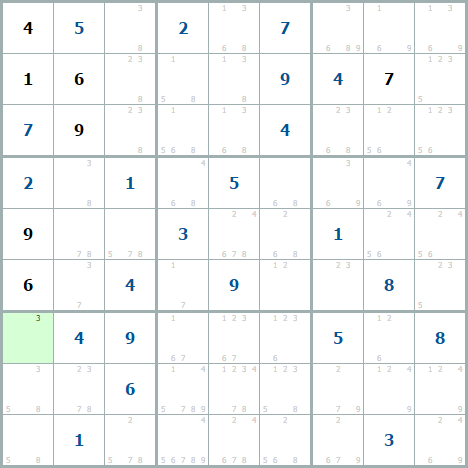
После удаления всех очевидно неподходящих кандидатов получилась клетка, где остался всего 1 кандидат (зеленая), значит, там это число – тройка, и стоит.
Так же числа ставятся, если кандидат остался последним в квадрате, строке или столбце:
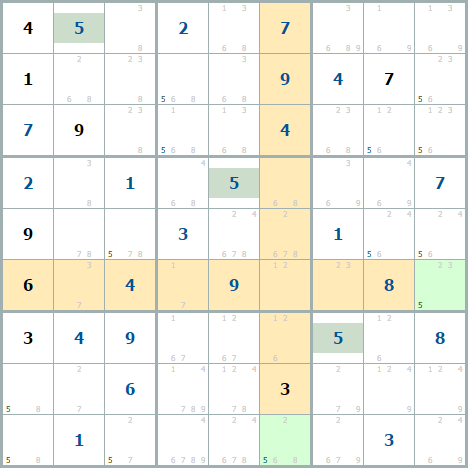
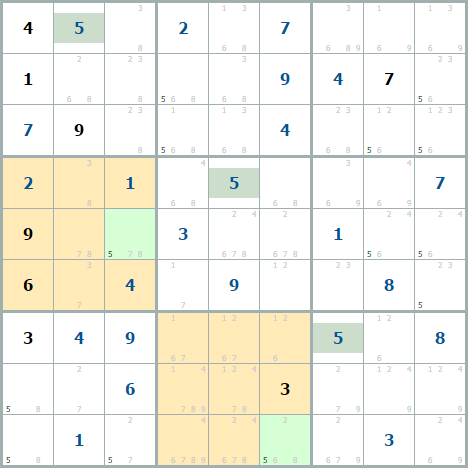
Это примеры на пятерках, можно увидеть, что в оранжевых клетках пятерок нет, а в зеленых клетках остается единственный кандидат в области, значит, пятерки там и стоят.
Это самые начальные способы простановки чисел в судоку, можно уже опробовать их, решая судоку на простой сложности (одна звезда), например: Судоку № 12433, Судоку № 14048, Судоку № 526. Указанные судоку полностью решаются с использованием информации выше. Но в случае, если не получается найти следующую цифру, можно прибегнуть к методу подбора – сохранить судоку, и попробовать наугад проставить какую-нибудь цифру, а в случае неудачи загрузить судоку.
Если хочется освоить более сложные методы, читайте далее.
Рассмотрим следующую ситуацию:

В квадрате, выделенном синим, кандидаты цифры 4 (зеленые ячейки) располагаются в двух клетках на одной линии. Если на этой линии (оранжевые клетки) будет стоять цифра 4, то в синем квадрате некуда будет поставить 4, значит – исключаем 4 из всех оранжевых клеток.
Аналогичный пример для цифры 2:
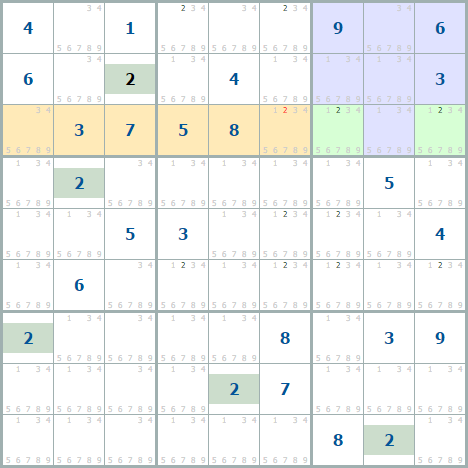
Этот пример похож на предыдущий, но здесь в строке (синяя) кандидаты 7 располагаются в одном квадрате. Это значит, что из всех оставшихся клеток квадрата (оранжевые) удаляются семерки.

Аналогично предыдущему примеру, только в столбце кандидаты 8 расположены в одном квадрате. Так же убираются все кандидаты 8 из других клеток квадрата.
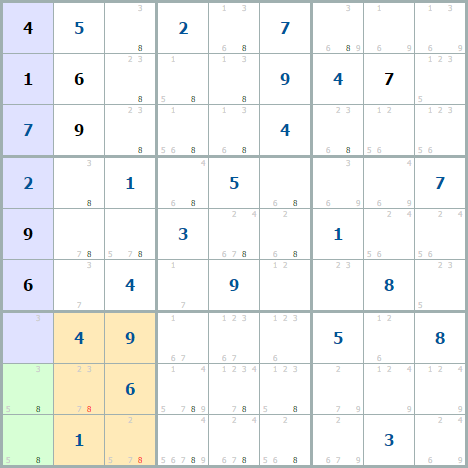
Освоив запертых кандидатов, можно решать судоку средней сложности без подбора, например: Судоку № 11466, Судоку № 13121, Судоку № 11528.
Группы увидеть сложнее, чем запертых кандидатов, но они помогают пройти многие тупиковые ситуации в сложных кроссвордах.
Самый простой подвид групп – это две одинаковые пары чисел в одном квадрате, строке или столбце. Для примера голая пара чисел [7, 8] в строке:
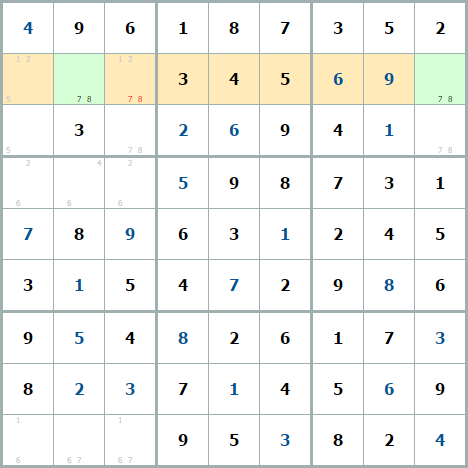
Если в любой другой клетке в оранжевой строке будет 7 или 8, то в зеленых клетках останется 7 и 7, либо 8 и 8, но по правилам невозможно, чтобы в строке было 2 одинаковых числа, значит все 7 и все 8 убираются из оранжевых клеток.
Еще пример:
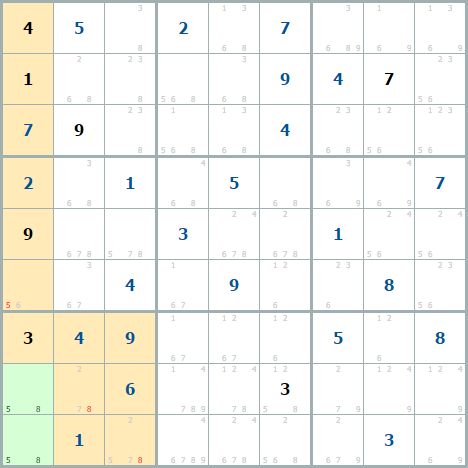
Голая пара [5, 8] одновременно в одном столбце и в одном квадрате. Удаляются лишние кандидаты (красные) и из столбца и из квадрата.
Важное замечание – группа должна быть именно «голой», то есть не содержать других чисел в этих клетках. То есть [5, 8] и [5, 8] являются голой группой, а [5, 6, 8] и [5, 8] – нет, так как группа уже не голая, есть лишнее число - 6. Так же [5, 8] и [5, 7] не являются голой группой, так как числа должны быть одинаковы, а здесь 3 разных числа в группе.
Голые тройки похожи на голые пары, но обнаружить их сложнее – это 3 голых числа в трех клетках.

В примере числа [1, 2, 6] в одной строке повторяются 3 раза. В группе всего 3 числа и они располагаются на 3-х клетках, значит лишние числа 1, 2, 6 из оранжевых клеток удаляются.
Голая тройка может не содержать числа в полном составе, например, подошла бы комбинация: [1, 6], [1, 2] и [2, 6] – это все те же 3 типа чисел в трех клетках, просто в неполном составе.
Следующее расширение голых групп – голые четверки.
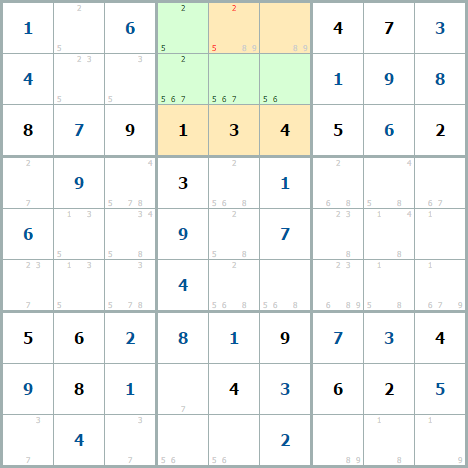
Числа [2, 5], [2, 5, 6, 7], [5, 6, 7], [5, 6] образуют голую четверку из четырех чисел 2, 5, 6 и 7, расположенных в четырех клетках. Эта четверка расположена в одном квадрате, это значит, что все числа 2, 5, 6, 7 из оставшихся клеток квадрата (оранжевые) удаляются.
Следующая вариация групп – скрытые группы. Рассмотрим пример:
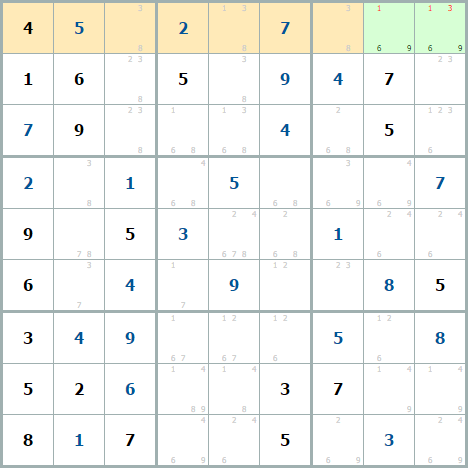
В самой верхней строке числа 6 и 9 расположены только в двух клетках, в других клетках этой строки таких чисел нет. И если в одной из зеленых клеток поставить другое число (например 1), то в строке не останется места для одного из чисел: 6 или 9, значит нужно удалить все числа в зеленых клетках, кроме 6 и 9.
В итоге, после удаления лишнего, должна остаться только голая пара чисел.
Аналогично скрытым парам – 3 числа стоять в 3-х клетках квадрата, строки или столбца и только в этих трех клетках. В этих же клетках могут быть другие числа – они удаляются
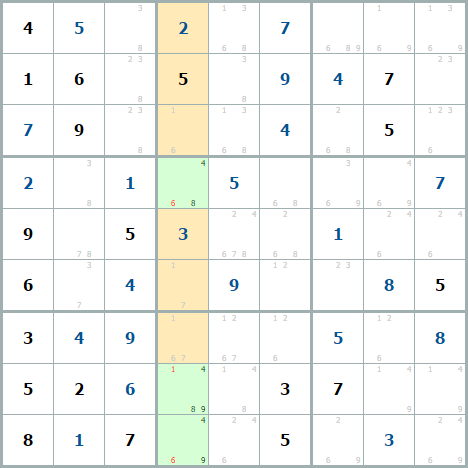
В примере скрываются числа 4, 8 и 9. В других клетках столбца этих чисел нет – значит удаляем лишних кандидатов из зеленых клеток.
Аналогично со скрытыми тройками, только 4 числа в 4-х клетках.

В примере четыре числа 2, 3, 8, 9 в четырех клетках (зеленые) одного столбца образуют скрытую четверку, так как в других клетках столбца (оранжевые) нет этих чисел. Удаляются лишние кандидаты из зеленых клеток.
На этом закончим рассмотрение групп чисел. Для тренировки попробуйте решить следующие кроссворды (без подбора): Судоку № 13091, Судоку № 10710
Эти странные слова – названия двух похожих способа исключения кандидатов в судоку.
X-wing рассматривается для кандидатов одного числа, рассмотрим 3:
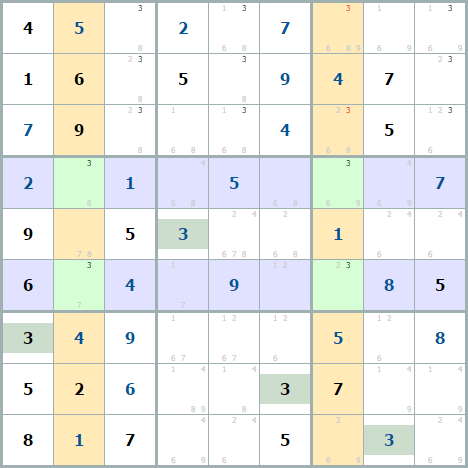
В двух строках (синие) расположены всего 2 тройки и эти тройки лежат всего на двух линиях. Данная комбинация имеет всего 2 решения по тройкам, а другие тройки в оранжевых столбцах противоречат этому решению (проверьте, почему), значит красные кандидаты на тройки должны быть удалены.
Аналогично для кандидатов на 2 и столбцов.
По факту X-wing встречается довольно часто, но не так часто встреча с этой ситуацией сулит исключение лишних чисел.
Рыба-меч
Это усложненная вариация X-wing для трех строк или столбцов:
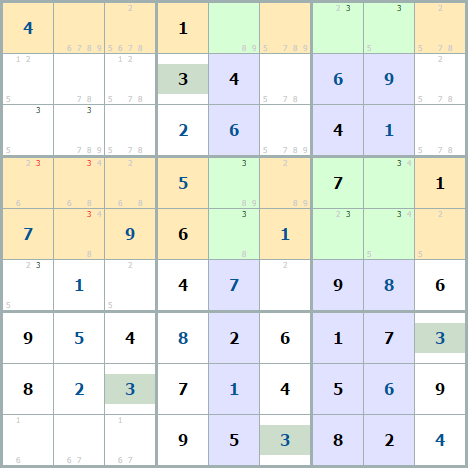
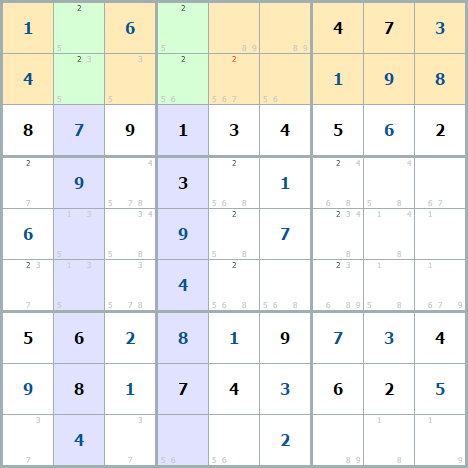
Рассматриваем так же 1 число, в примере это 3. 3 столбца (синие) содержат тройки, которые принадлежат к одним и тем же трем рядам.
Числа могут содержаться не во всех клетках, но нам важно пересечение трех горизонтальных и трех вертикальных линий. Либо по вертикали, либо по горизонтали должны отсутствовать числа во всех клетках, кроме зеленых, в примере это вертикаль – столбцы. Тогда все лишние числа в строках должны быть убраны, чтобы 3 остались только на пересечениях линий – в зеленых клетках.
А так же ответ на вопрос: почему не ищут скрытые/голые пятерки, шестерки итд?
Давайте рассмотрим следующие 2 примера:
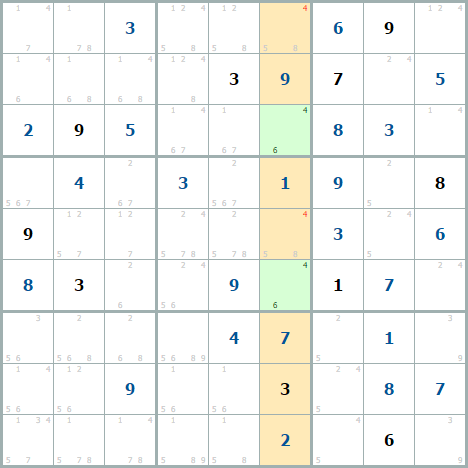
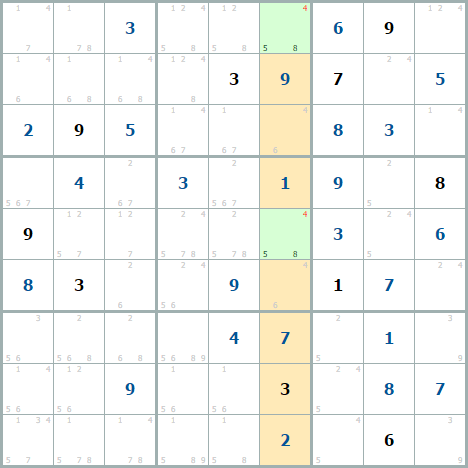
Это один судоку, где рассматривается один числовой столбец. 2 числа 4 (отмечены красным) исключаются 2 разными способами – при помощи скрытой пары или при помощи голой пары.
Следующий пример:
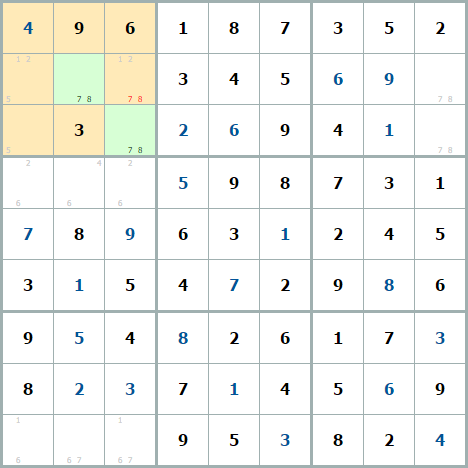
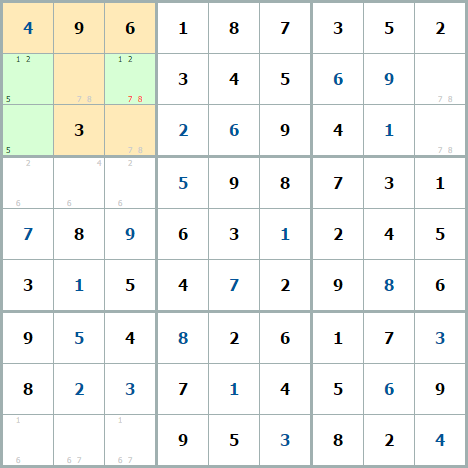
Другой судоку, где в одном квадрате одновременно голая пара и скрытая тройка, которые удаляют одни и те же числа.

Если вы присмотритесь в примеры голых и скрытых групп в предыдущих параграфах, то заметите, что при 4-х свободных клетках с голой группой оставшиеся 2 клетки обязательно будут голой парой. При 8-и свободных клетках и голой четверке – оставшиеся 4 клетки будут скрытой четверкой:
Если рассмотреть взаимосвязь голых и скрытых групп, то можно выяснить, что при наличии голой группы в оставшихся клетках обязательно будет скрытая группа и наоборот.
И из этого можно сделать вывод, что если у нас свободны 9 клеток в строке, и среди них точно есть голая шестерка – то проще будет найти скрытую тройку, чем выискивать взаимосвязь между 6-ю клетками. Так же со скрытой и голой пятеркой – легче отыскать голую/скрытую четверку, поэтому пятерки даже не ищутся.
И еще один вывод – искать группы чисел имеет смысл только при наличии хотя бы восьми свободных клеток в квадрате, строке или столбце, при меньшем количестве клеток можно ограничиться скрытыми и голыми тройками. А при пяти свободных клетках и меньше можно не искать тройки – двоек будет достаточно.
Здесь приведены самые известные методы разрешения судоку, но при решении сложных судоку далеко не всегда применение этих методов ведет к полному решению. В любом случае метод подбора всегда придет на помощь – сохраняете судоку в тупиковом месте, подставляете любое доступное число и пытаетесь решить головоломку. Если эта подстановка приводит вас к невозможной ситуации, то значит, что нужно загрузиться и убрать подставленное число из кандидатов.
 6
6
 0
0

 13
13
 14
14




